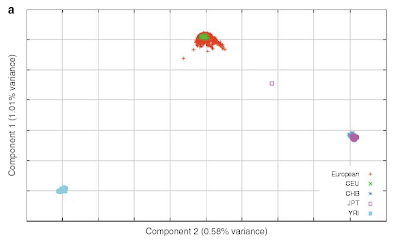
Figure: The three clusters shown above are European (top, green + red), Nigerian (light blue) and E. Asian (purple + blue).
The figure seems to contradict an often stated observation about human genetic diversity, which has become known among experts as Lewontin's fallacy: genetic variation between two random individuals in a given population accounts for 80% or more of the total variation within the entire human population. Therefore, according to the fallacy, any classification of humans into groups ("races") based on genetic information is impossible. ("More variation within groups than between groups.")
To understand this statement better, consider the F statistic of population genetics, introduced by Sewall Wright:
Fst = 1 - Dw / Db
Db and Dw represent the average number of pairwise differences between two individuals sampled from different populations (Db = "difference between") or the same population (Dw = "difference within"). Even in the most widely separated human populations Fst < .2 so Dw / Db > .8 (roughly). This may not sound like very much genetic diversity, but it is more than in many other animal species. See here for recent high statistics Fst values by nationality.
Dw / Db > .8 means that the average genetic distance measured in number of base pair differences between two members of a group (e.g., two randomly selected Europeans) is at least 80 percent of the average distance between distant groups (e.g., Europeans and Asians or Africans). In other words, if two individuals from very distant groups (e.g., a Japanese and a Nigerian) have on average N base pair differences, then two from the same group (e.g., two Nigerians or two Japanese) will on average have roughly .8 N base pair differences.
How can the Fst result ("more variation within groups than between groups") be consistent with the clusters shown in the figure? I've had to explain this on numerous occasions, always with great difficulty because the explanation requires a little mathematics. In order to make the point more accessible, I've created the figures below, which show two population clusters, each represented by an ellipsoid (blob). The different figures depict the same pair of objects, just viewed from different angles.
The blobs are constructed and arranged so that the average distance between two points (individuals) within the same cluster is almost as big as the average distance between two points (individuals) in different clusters. This is easy to achieve if the ellipsoids are big and flat (like pancakes) and placed close to each other along the flat directions. The figure is meant to show how one can have small Fst, as in humans, yet easily resolved clusters. The direction in which the gap between the clusters appears is one of the principal components in the space of human genetic variation, as recently found by bioinformaticists. The figure at the top of this post plots individuals as points in the space generated by the two largest principal components extracted from the combination of data from HapMap and from large statistics sampling of Europeans. Exhibited this way, isolated clusters ("races") are readily apparent.
The real space of genetic variation has many more than 3 dimensions, so it can't be easily visualized. But some aspects of the figures below still apply: there will be particular directions of variation over which different populations are more or less identical (orthogonal to the principal component; i.e. along the flat directions of each pancake), and there will be directions in which different populations differ radically and have little or no overlap. Note, however, that we are specifically referring to genetic variation, which may or may not translate into phenotypic variation.


Related posts: "no scientific basis for race" , metric on the space of genomes.
The existence of this clustering has been known for 40 years.









